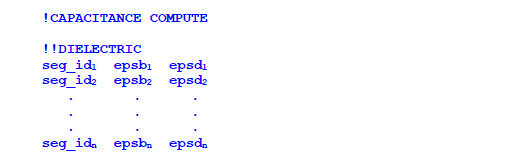
Capacitance Compute

The purpose of this keyword is to specify the automatic computation of both the cable capacitance matrix parameters and the associated cable inductance matrix parameters. These parameters can be computed from the geometric location of the conductors in the segment. The conductor layout must be defined by the SEGMENT/COMPLEX or the SEGMENT/COMPLEX2 keyword combination pairs discussed in Section 8.4. The CAPACITANCE COMPUTE keyword described here provides additional geometric and material parameter information necessary to compute the capacitance parameters/matrices. For the outermost shielding level, the ground plane, at 0.0=z, is taken to be the default reference conductor. For shielded conductors, the associated shielding conductor is taken to be the reference conductor. If the default references are not the desired selections, then another reference can be specified (see Section 8.11).

There are three associated second level keyword. These are listed below.

1) DIELECTRIC

2) RADII

3) FILAMENT NUMBER

All three of these keywords should be present if the CAPACITANCE COMPUTE keyword is used. Each of these keywords provides necessary information required for the automatic computation of the capacitance matrix.

This keyword is used to specify the number of charge filaments designated to characterize the charge distribution on the various conductors within a cable segment to facilitate capacitance matrix computations. A diagram of the cross-section of two conductors is shown in Figure 8.6.2.1. One conductor has fifteen designated charge filaments, the other conductor five. The charge filaments are at equal angular increments around the circumference of each conductor. These charge filaments represent lines of constant charge along the length of each conductor. The actual charge distribution on each wire is therefore characterized by a discrete number of filaments. The more filaments that are used on each wire, the better the charge characterization. However, as the number of filaments increases, the greater amount of time required to compute the capacitance matrix.

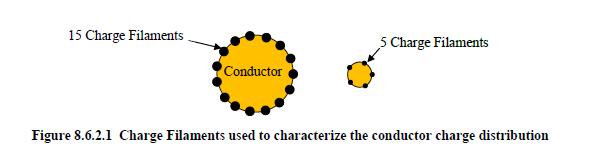
The ramification of filament number selection should be understood. As the distance between conductors increases, the number of filaments required to accurately represent the charge distribution generally decreases. As the distance between conductors decreases, the number of filaments required for accurate characterization generally increases. This is especially true when a small diameter conductor is near a large diameter conductor. If the small diameter conductor in Figure 8.6.2.1 is move closer to the large diameter conductor, the charge distribution on the latter would vary greatly on the surface close to the small conductor. To accurately characterize this type of distribution, more filaments may be required.